Energiatrilemma teine komponent on keskkonnasäästlikkus.
Keskkonnasäästlikus väljendab energiasüsteemi suutlikkust leevendada ja vältida keskkonna ning kliimamuutusi tekitavaid mõjusid. All on toodud WEC (World Energy Council) hinnang Eestile 2022. aastal. Eesti trilemma koguskoor oli 2021. aastal 73,9 ning 2022. aastal saavutas Eesti koguskoori 78,7, millega oleme 9 kohal, hinnatud riikidest.
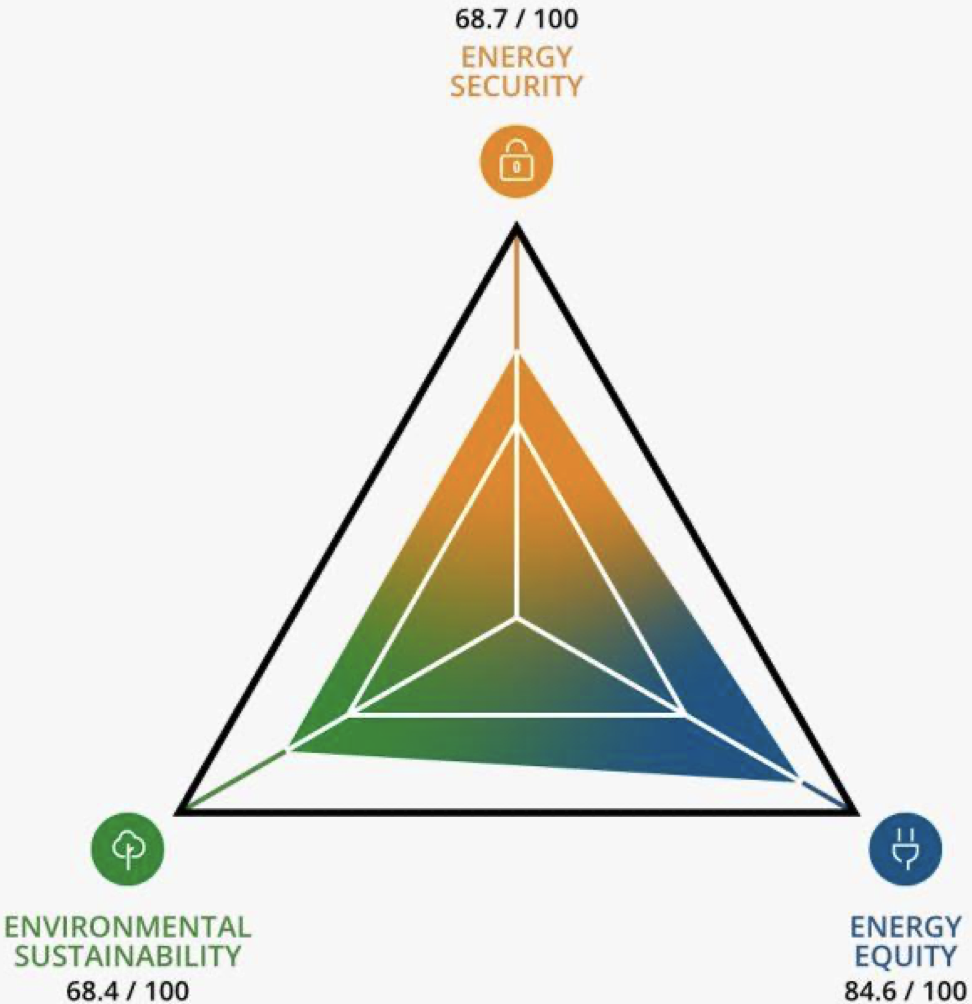
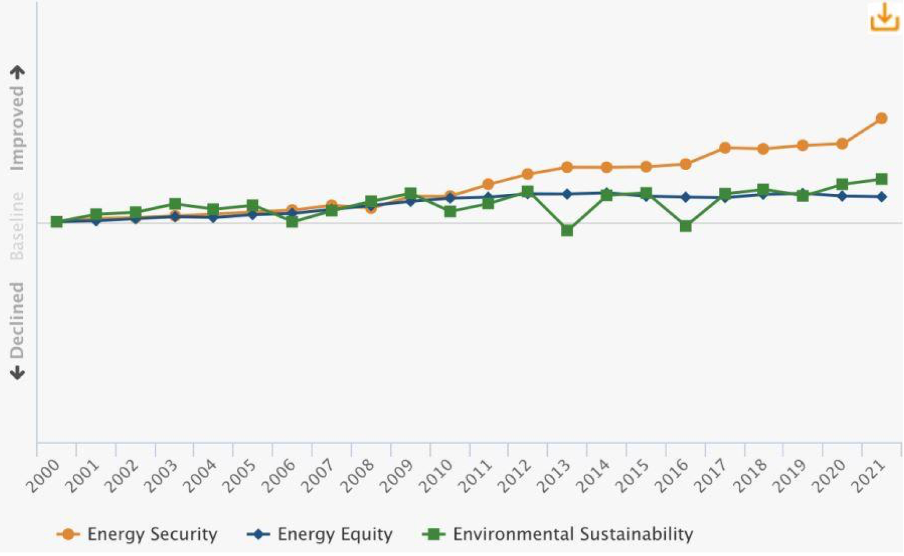
Allikas: https://www.akadeemia.ee/wp-content/uploads/2022/05/priit-mandmaa.-30.05.2022.pdf
Täpsemalt võib toodud hinnangu kohta lugeda lehelt: https://wec-estonia.ee/world-energy-trilemma-index-2022/
Kliimaeesmärgid
Eesti osana Euroopa Liidust on seadnud ambitsioonikad eesmärgid kliimaneutraalsuse saavutamiseks. Juba aastaks 2030. on Euroopa Liidu ülene eesmärk vähendada kasvuhoonegaaside (KHG) netoheidet -55% võrreldes 1990. aastaga. Aastaks 2050 soovitatakse saavutada kliimaneutraalsus.
Tee kliimaneutraalsuseni hõlmab laiapõhist tegutsemist. Tegutseda tuleb seitsmes strateegilises valdkonnas: energiatõhusus, taastuvate ressursside kasutuselevõtt, turvaline ja ühendatud liikuvus, konkurentsivõimeline tööstus ja ringmajandus, infrastruktuur ja ühendused, biomajandus ja looduslikud süsinikusidujad, süsinikdioksiidi kogumine ja säilitamine.
Rohkem infot kliimaeesmärkide kohta leiad: https://kliimaministeerium.ee/euroopa-liidu-kliimaeesmargid
Hoonete energiatõhusus
Kui riiklik energiapoliitika on valdkond, mis võib paljude jaoks jääda kaugeks, siis kodude energiatõhusus on see, millega tihti kokku puututakse. Näiteks on uut kodu otsides tasub vaadata hoone energiamärgist riiklikust ehitisregistrist https://livekluster.ehr.ee/ui/ehr/v1/
Tihti on välja toodud kaks näitajat: KEK ja ETA
KEK ehk kaalutud energiaerikasutus on tegelikel tarbeandmetel põhinev energiakandjate kaalumisteguritega korrutatud aastane energiakasutus. Ühik: kWh/m2a
ETA ehk energiatõhususarv on arvutuslik summaarne tarnitud energiate kaalutud erikasutus hoone tüüpilisel kasutusel. ETA koostatakse uutele hoonetele või hoonetele, mida oluliselt rekonstrueeritakse.
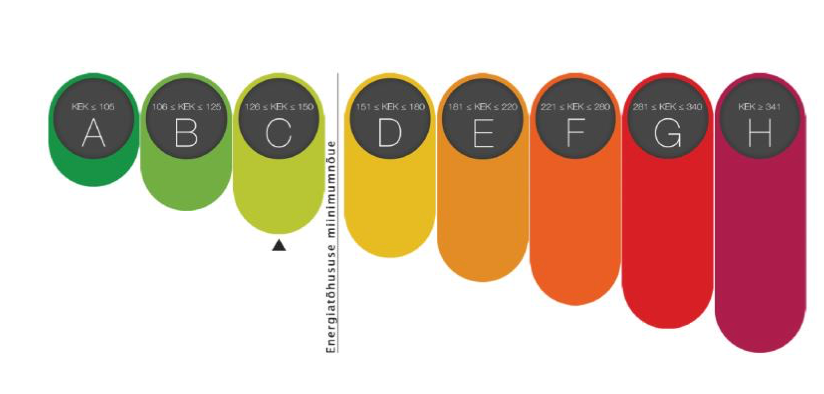
Energiamärgise klassid
Allikas: Kredex (https://kredex.ee/sites/default/files/2021-05/Hoonete%20energiatõhusus%2004.05.2021.pdf)
Täpsem info hoonete energiamärgise andmise kohta on leitav: https://www.riigiteataja.ee/akt/106052015002
Süsinikujalajälg ja kestlikkus
Esimene samm keskkonnasõbralikkuse parandamiseks on hetkeolukorra kaardistamine. Ilma hetkeolukorda teadmata on raske aru saada, mida on vaja teha. Eestis on kasvuhoonegaaside jalajälje leidmiseks loodud arvutusmudel, mis võimaldab kasutada Eesti spetsiifilist infot.
Täpsem info KHG jalajälje leidmiseks on leitav: https://kliimaministeerium.ee/organisatsioonide-khg-jalajalg
Ülesanded
Ülesanne 1:
Maril on kodus 25 m2 vaba pinda, kuhu saab panna päikesepaneeli ning tal on fikseeritud elektripakett, kus elektrihind on 0,15 eurot/kWh, kuid Mari mõtles, et lisaks võiks panna ka päikesepaneeli, mille abil ostetava elektrienergia hulka vähendada. Mari leidis päikesepaneeli infolehe, kus oli kirjas, et päikesepaneel on taastuvenergialahendus, mis suudab 1 kW kohta toota aastas ligikaudu 1 MWh elektrienergiat ning päikesepaneel suudab töötada aastakümneid, küll väheneb aga vaikselt iga-aastane toodang, tootjapoolt oli toodud selleks 1% aastas. Tootja poolt oli ka kirjas, et 1 kW päikesepaneeli rajamiseks on vaja 5 m2 vaba pinda. Investeering tundus ka Marile igati mõistlik, 1kW päikesepaneeli maksab 700 eurot.
a. Mis on paigaldatavate paneelide lihttasuvusaeg?
b. Mis juhtub tasuvusajaga, kui Mari suudab leida parema elektripaketi ja tema uus elektrihind on 0,10 eurot/kWh? (too ka numbriline väärtus)
c. Kui palju toodavad paneelid aastas energiat kui paigaldusest on möödunud 30 aastat?
Ülesanne 2:
Maiel on korter, mille pindala on 50 m2. Korteris kasutatakse aastas 1377 kWh elektrit, millel puudub taastuvenergia päritolutunnus ning soojuse tootmiseks kasutatakse aastas 550 m3 maagaasi.
a. Leida mis on hoone kaalutud energiakasutus ja sellele vastav energiaklass?
b. Mis on korteri KHG heide?
c. Millist kütteliiki kasutades oleks võimalik saavutada ühe energiaklassi võrra parem energiaklass?
d. Kui Maie tarbiks sertifitseeritud taastuvelektrit, siis kui palju väheneks KHG jalajälg võrreldes alginfoga?
Kasulikke linke:
Kliimaministeeriumi KHG jalajälje arvutusmudel
Vastuste saab esitada kuni 12. november 23.59 : https://forms.gle/cCENRDBtDaX6fScc8